这是SIGGRAPH Asia 2021 的论文,也是ACM Transaction of Graphics的论文。其实基础的MC算法也是图形学常用底层算法之一,研究研究也挺好的~
PPT:https://icys.top/reveal-0406/
起源——Marching Cubes
说到Marching Cubes,朋友给我发了张图,表示这就是Marching Cubes(图片来自于YouTube Code Adventure频道)。

Marching Cubes (通常缩写为MC)算法是1987年发明的等值面提取算法,也是迄今为止使用最多的提取方法。当时原论文利用原始的三维数据推导内切片的连通性、表面位置和表面梯度,通过分而治之,得到相对高质量的结果。
MC算法把按均匀晶格(Grid)采样的隐式场作为输入,并提取表示场的零等值面的三角形网格(Mesh)。
在图形学中,曲线曲面等的表示,分为显式表达和隐式表达。显式表达就是能写出一个类似于$z=x^2+y$的表达式,其中一个维度作为因变量,其他维度作为自变量,可以写出一个等价的关系,而隐式表达则是类似于$F(x, y, z)=0$的形式。从显式表达到隐式表达是非常简单的(移项就有了)。一些例如球、椭球等曲面就又可以显式表达也可以隐式表达,但是更多的复杂的曲面是很难有其显式表达的,我们就常用一个隐式距离场来进行表达,即对自变量组成的线性空间进行均匀间隔采样,通过三线性插值(在X、Y、Z坐标依次按顺序进行插值)来确定这个隐式表达的面。
在图形学中,三维物体常用Mesh结构表示,结构将连续的表面离散化,用多个三角面片(有的会用多边形)来表示曲面,这样会造成一定的精度误差。因此各种方法就是在尽可能地向准确值逼近,以更好地还原物体。
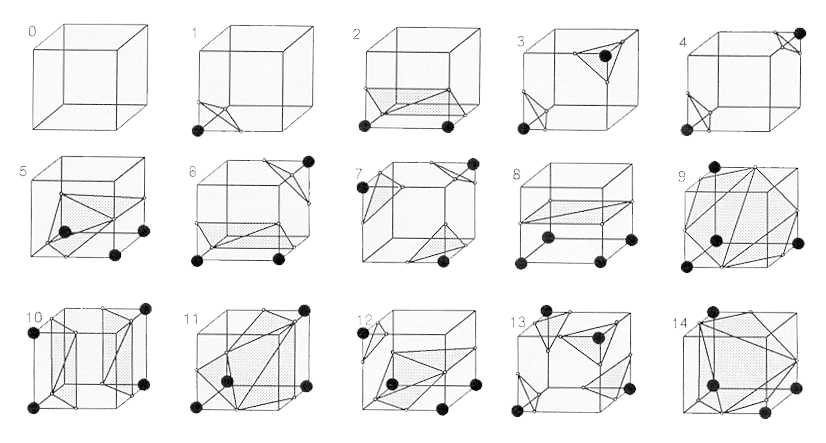
1987年发明的MC算法是最经典的做法,它通过检测一个立方体对应的八个顶点的符号,结合已有的预定义查找表格(在去除对称、旋转等变式后,论文总结出15种情况),确定这个立方体中的Mesh表示。当等值面与立方体边相交,将该边线性插值的点加入最后的顶点集合中。立方体一步一步依次移动(或者说前进March,这也是为什么叫做Marching Cubes),最后得到整个物体的面片结构。

改进——MC33
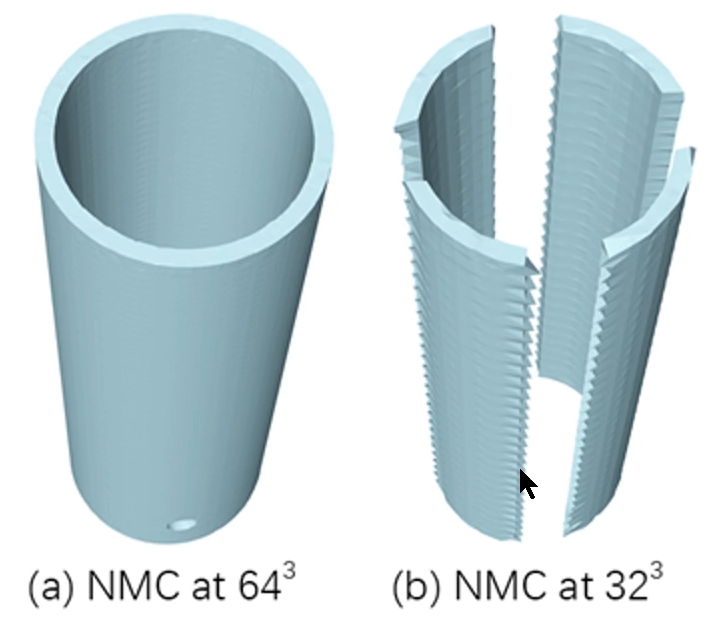
基础的MC算法在计算的时候,由于过度的分而治之,导致相邻两个立方体的面片结构不连续,使得生成出的结构带有孔洞(见下左图)。此外,基础的MC算法无法形成管道结构,对于真实物体的还原性有限(下右)。基于此,1995年,Chernyaev发表了MC33论文,对已有的MC算法进行优化,以保证拓扑的正确性。
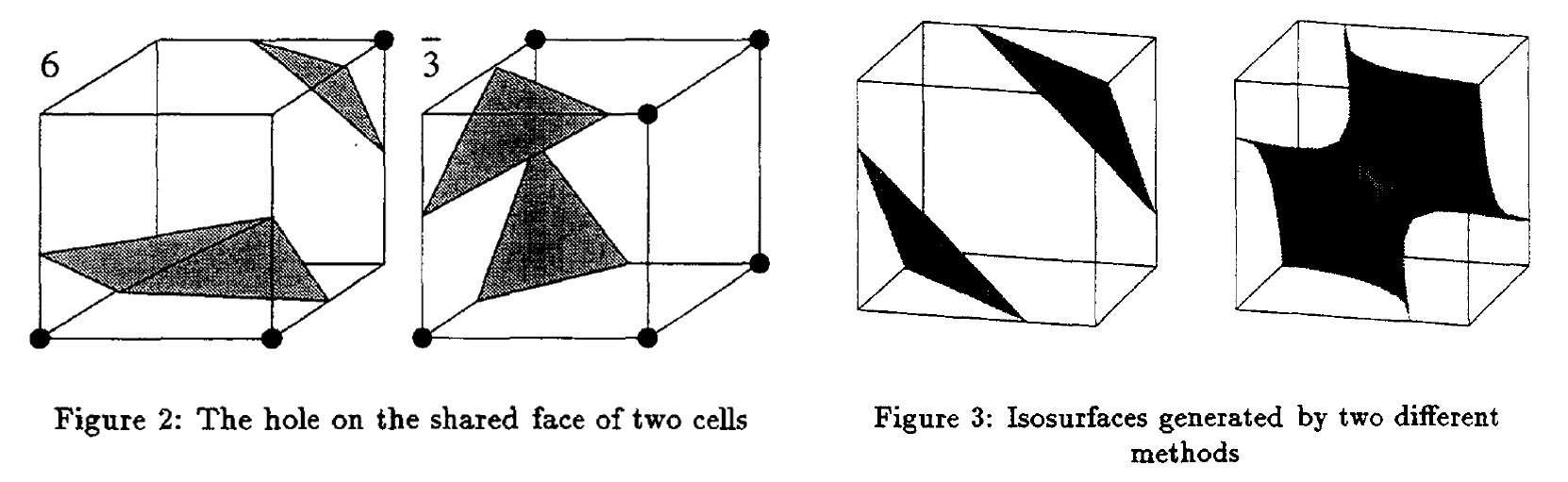
MC33的论文假设每个立方体的顶点不仅限于正负,可以使用三线性插值(按三个方向依次插值)以精确最后得到的结果。这篇论文发现,原来的15种结构中,平面内对角相同的2正2反正方形有两种(一个原象有两个象无法形成映射关系),称其为Ambiguous face,并且在相同立方体排布下仍可能存在多种情况,称其为Internal Ambiguity。
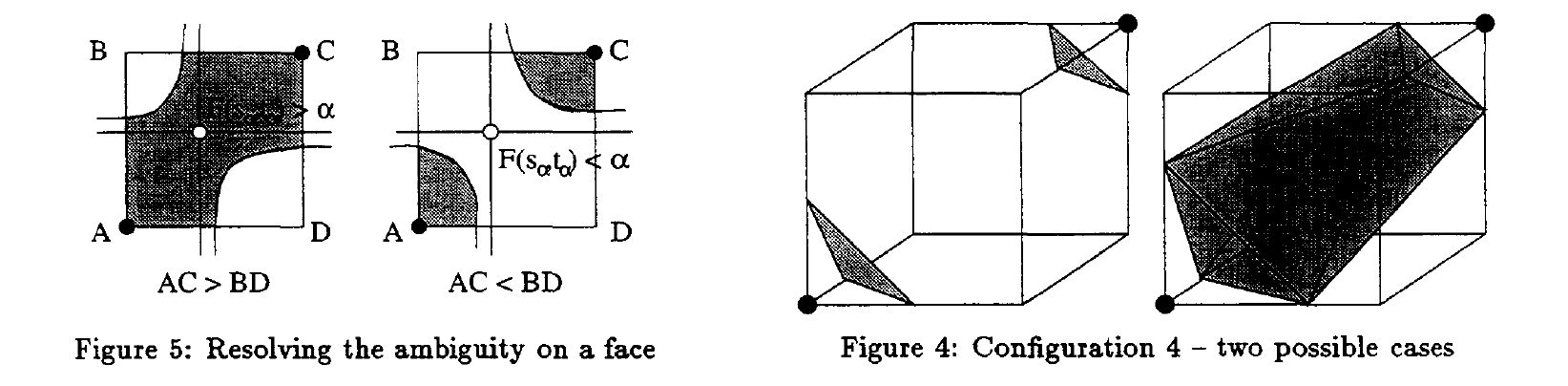
为了解决上述问题,确保在三线性插值基础上的拓扑正确性,论文细化了分类,将当前状态与相邻立方体结构情况相结合一并考虑,得到了33种立方体,具体结构如下:
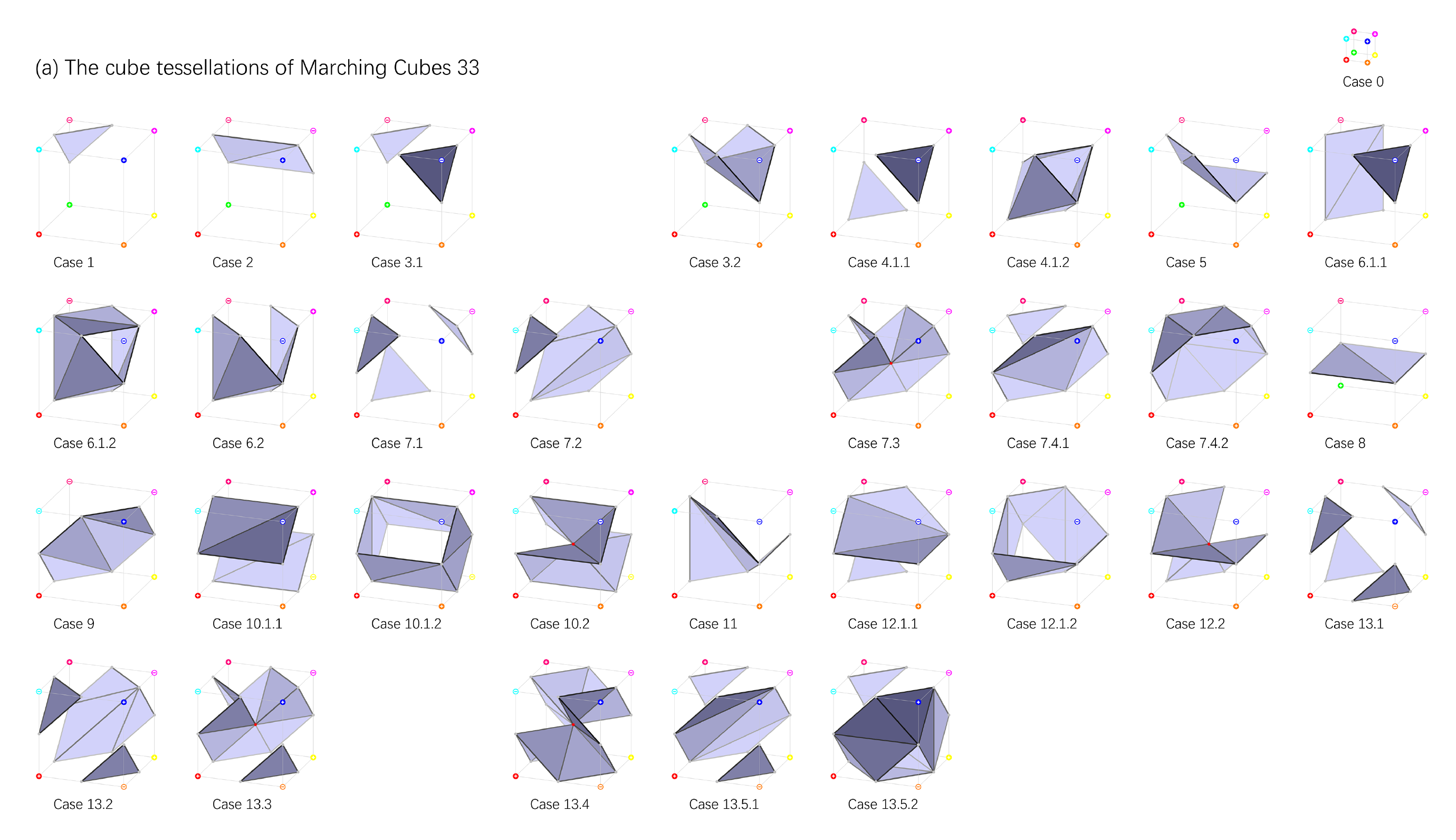
主菜——NMC
在若干年的发展中,MC方法修修补补,但仍没有完全解决一个比较棘手的问题——MC算法对于尖锐边缘的还原性不佳。近期有一些算法可以解决尖锐边缘问题,但是需要额外的输入。
于是自称加拿大最强的图形学高校SFU(况且称呼它为顺丰大学)的张皓团队,提出了深度学习的MC算法NMC,设计了兼容于传统MC算法的立方体结构表示方法,修改了一部分镶嵌方案(加入了一些隧道的情况),设计数据集并使用有监督的深度学习(基于ResNet网络模型)代替MC33的三线性插值方案,以获得更好的(尤其是可以更好表现边缘锐度的)物体重建效果。
效果预览
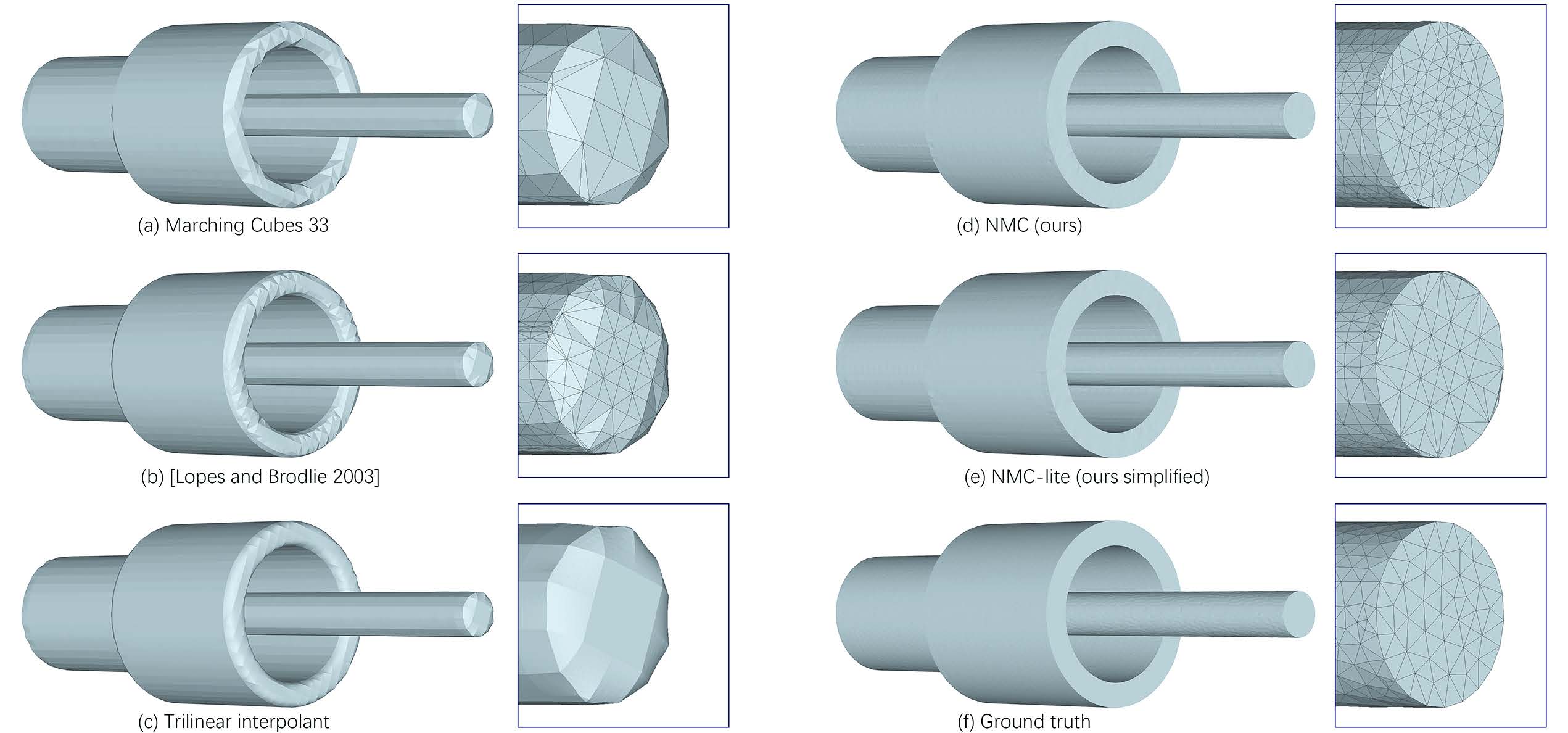
除了论文宣称的边缘锐利明显以外,可能有些(审稿)人会问,这个方法为了解决表现锐度边缘问题,那对于比较平滑的表面,效果怎么样呢?论文在补充材料里给出了效果对比(每一列的标签在图片最下方)。
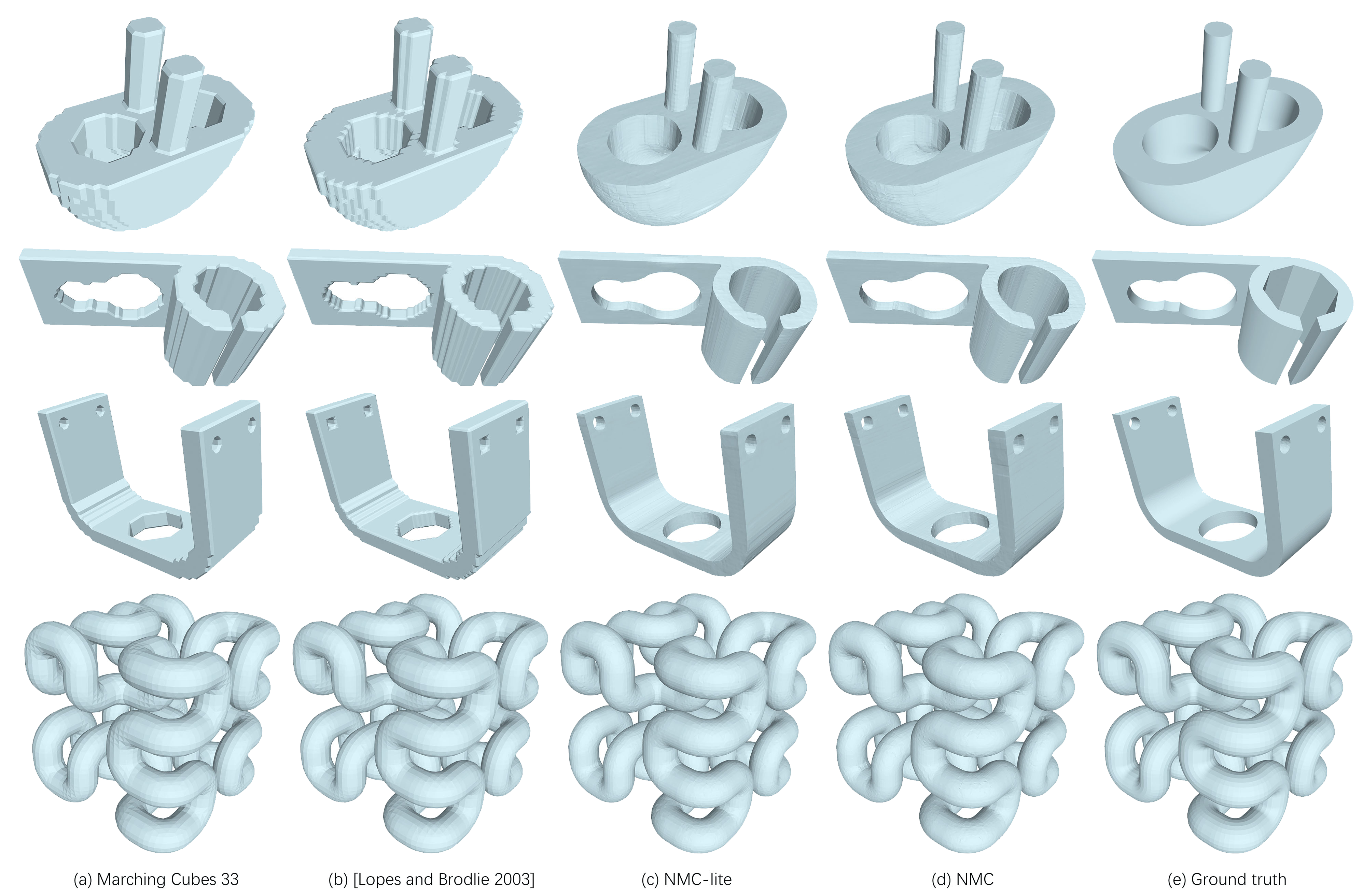
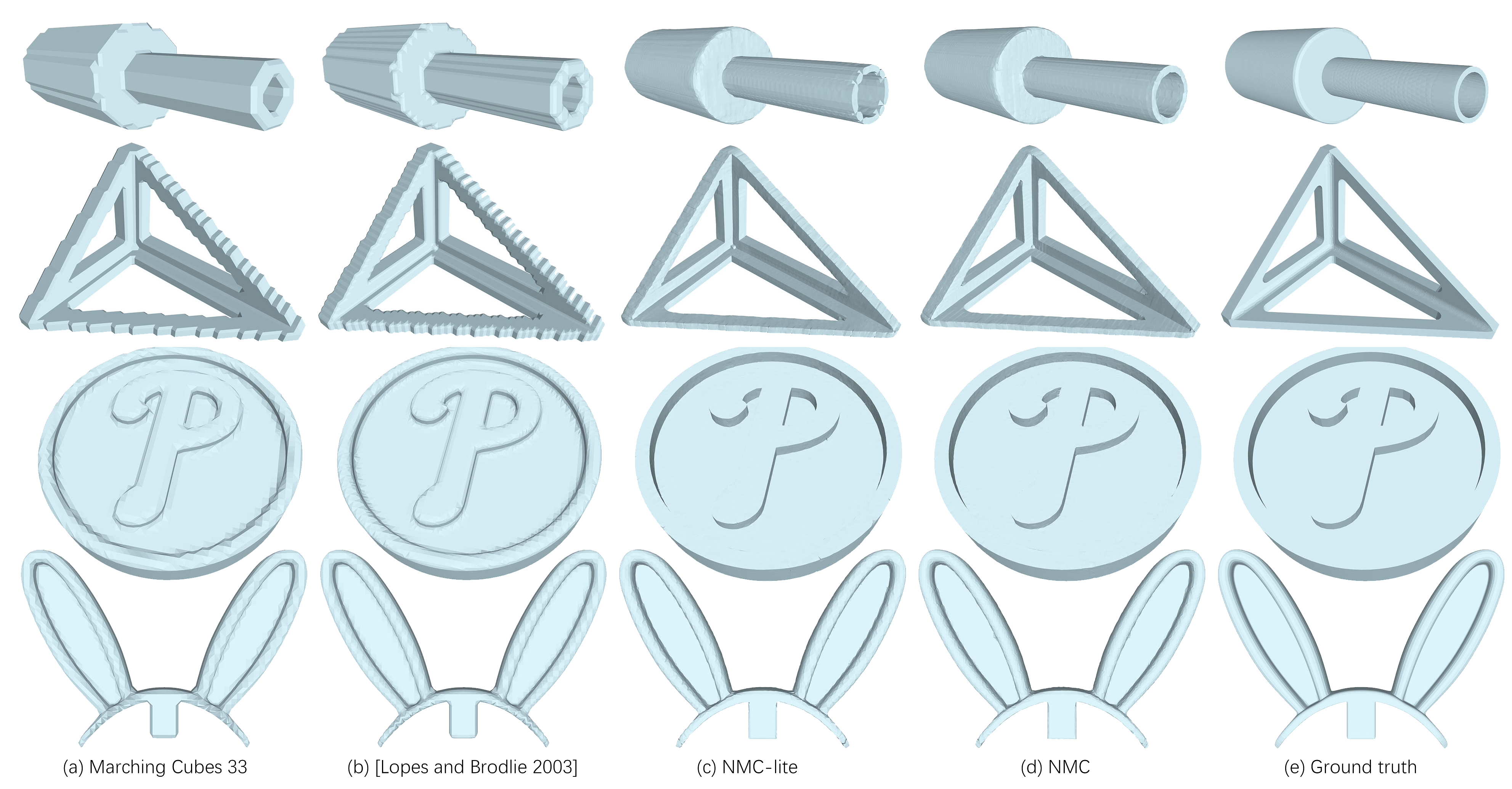
表示输出的Mesh结构
我们很希望深度学习网络输入一个隐式距离场(其实论文还可以输入体素结构),输出一个Mesh,但生成Mesh不太现实,那如何用深度学习网络的输出表示Mesh呢?
有一个Naive的表达方式,使用One-hot Vector表示每个立方体单元是每种镶嵌情况的概率,这样会使得训练效率非常低,而且不太好表示旋转对称等(否则会让向量的编码更长),不是一个明智的表达方式。
论文提出了一个新的表达方式,它从二维进行举例,并顺其自然地扩展到三维。对于MC算法的二维情况,论文在正方形中间加入四个自由的点,根据四角点的正负情况,这四个自由点会有1至2个点有效,参与形成的Mesh的顶点连接。此外,论文摒弃了传统的线性插值方法,将四条边上各加上一个有自由度的点(现在一共有$4+4=8$个点)。此时,对于一个正方形的嵌入方案,需要5个布尔值表示分别表示四角的正负情况和对角情况的正负面情况(刚才说一对二无法形成映射,则对于这种情况额外加一个布尔变量进行区分),还需要12个浮点数表示八个点的自由度(四条边上的点各有一个自由度,而正方形内的点各有两个自由度,共有$4\times1+4\times2=12$个自由度)。
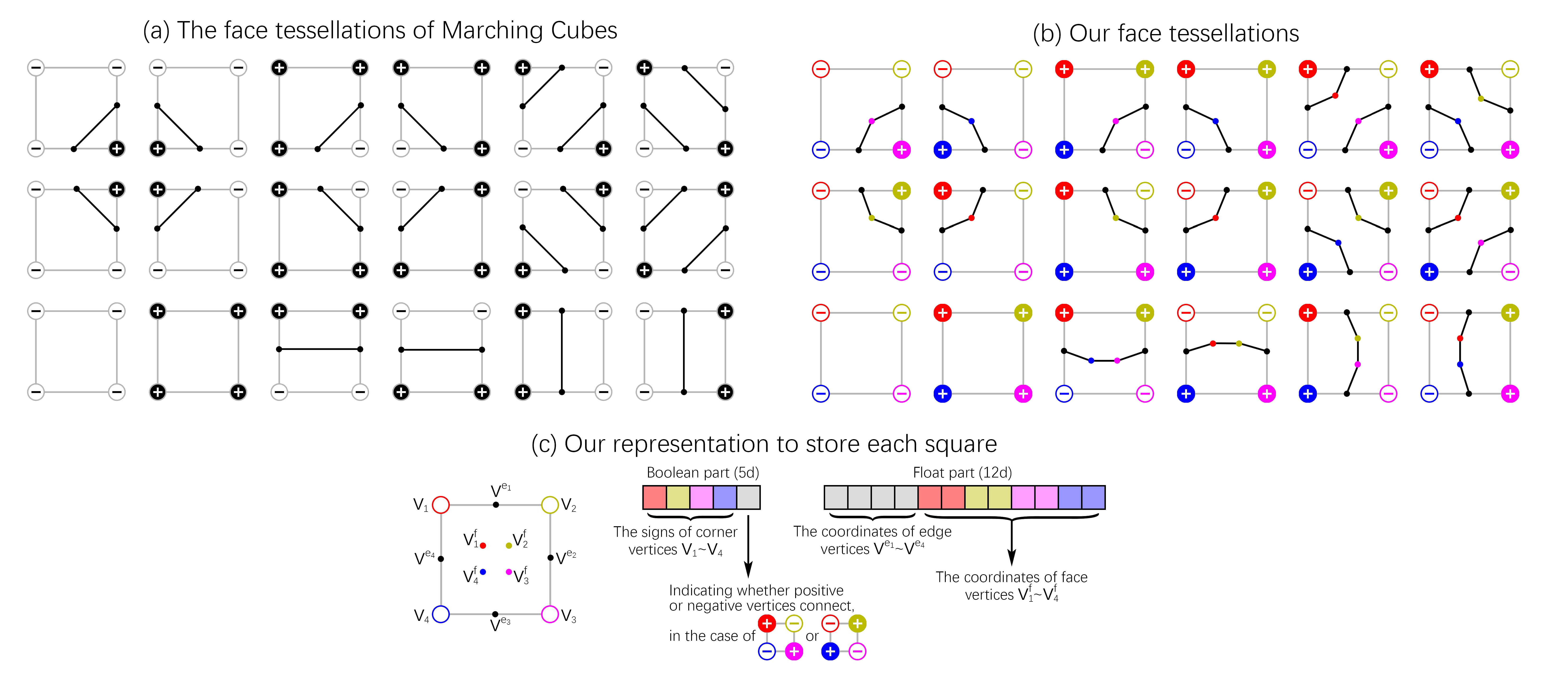
由于正方形不是独自存在,相邻正方形共用一边,一个顶点至多被四个正方形共用,故我们在表达时只表达每个正方形左上角顶点,以及上、左两边(最后一行一列加空padding就行了),这样一个正方形需要两个布尔值和10个浮点数进行表达(正方形内的点没有被共用)。
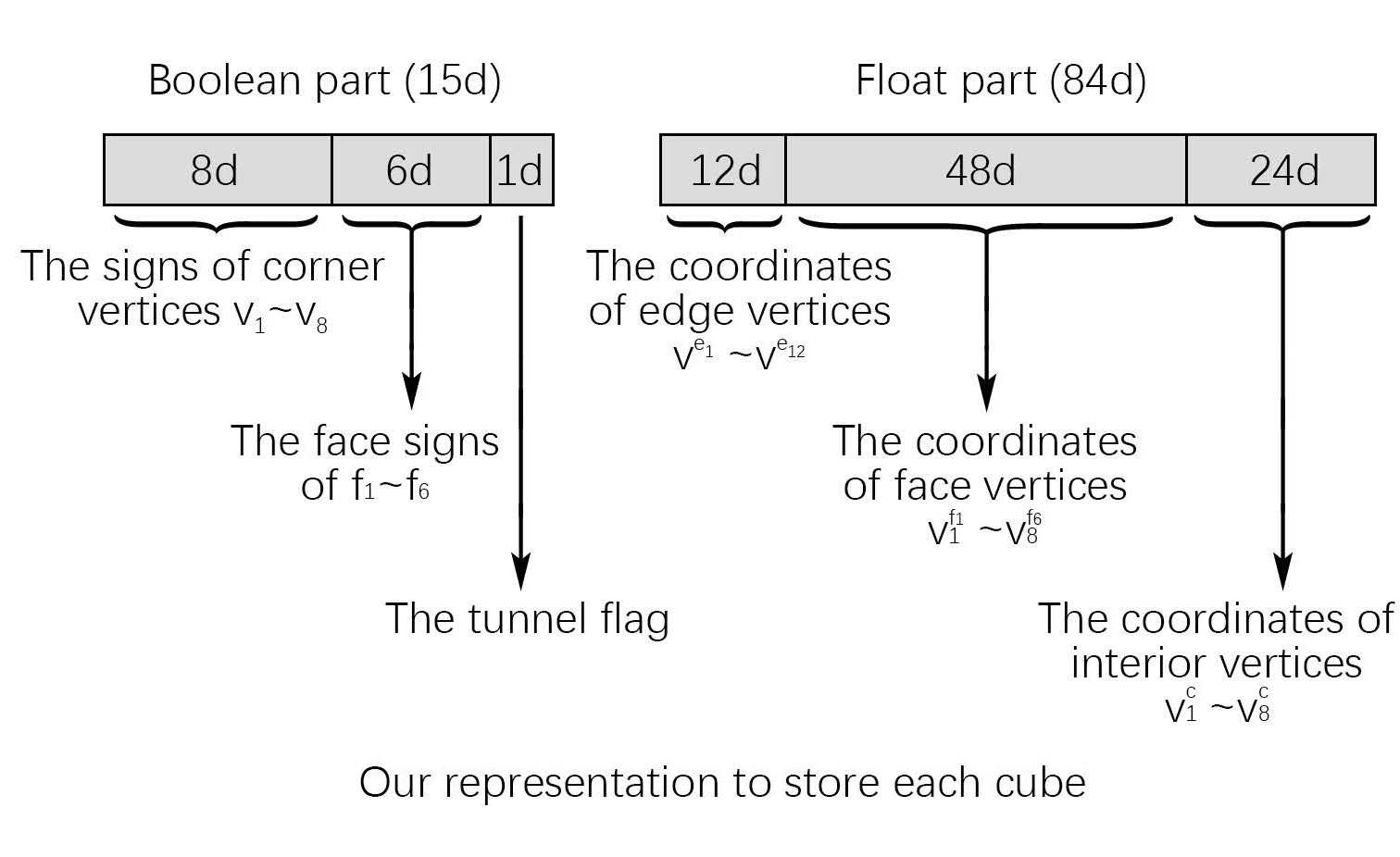
扩展到三维的时候,与二维同样的,每条边有一个自由度为1的点,每个面有4个自由度为2的点,此外还有体内8个自由度为3的点。此时表示一个立方体需要15个布尔值,分别表示8个顶点正负、6个面朝向(同正方形面朝向、仅在对角相同的情况使用)和一个Tunnel flag(与MC33相同,表示这个格子内是否存在隧道。因为论文仅考虑出现一个隧道的情况,所以只需要一个布尔值),需要84个浮点数,分别表示84个自由度($12\times1+6\times4\times2+8\times3=84$)。同样地,删节后,需要存储5个布尔值(1个顶点、三个面和隧道标志)和51个浮点数($3\times1+3\times4\times2+8\times3=51$)。
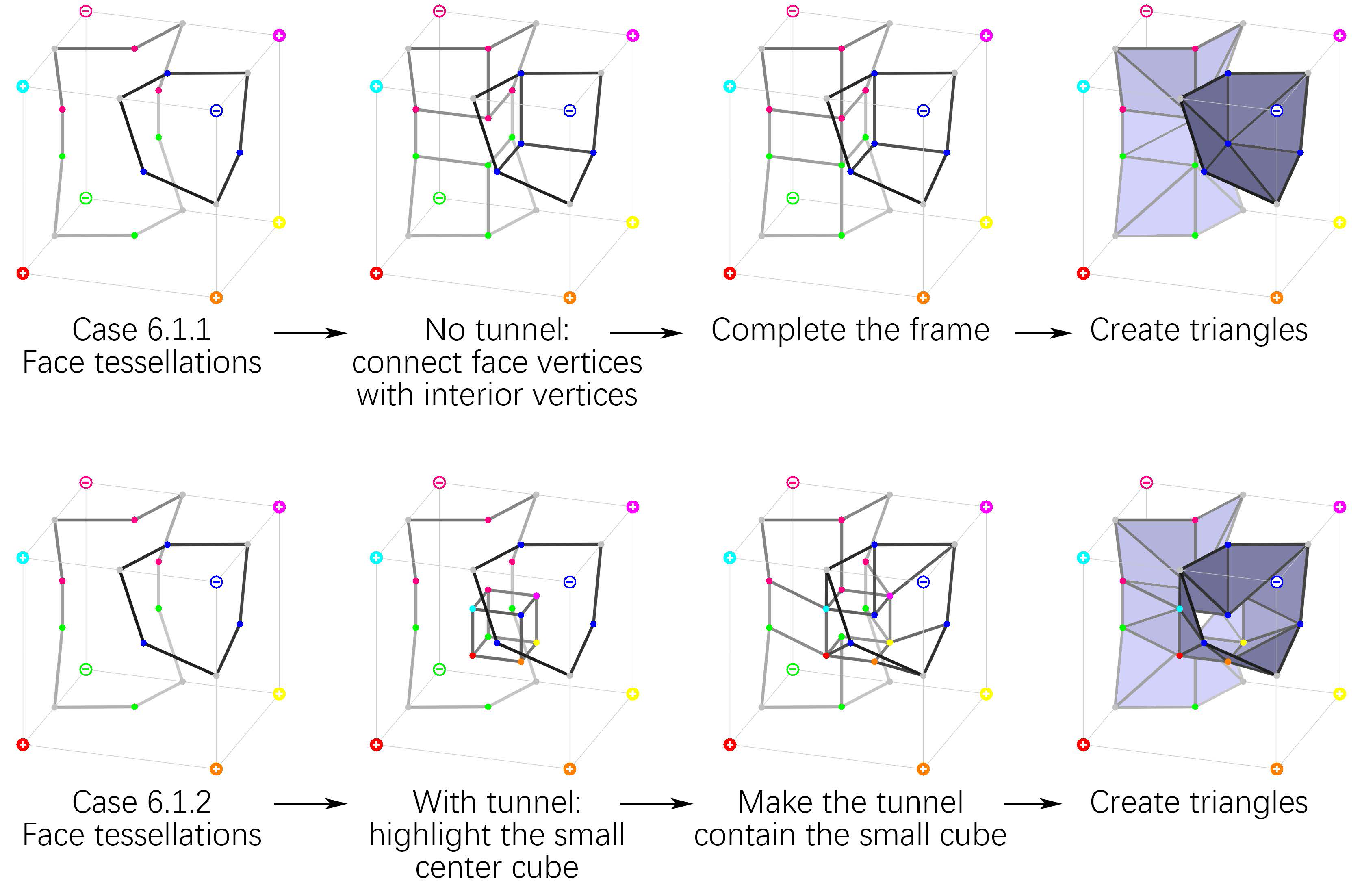
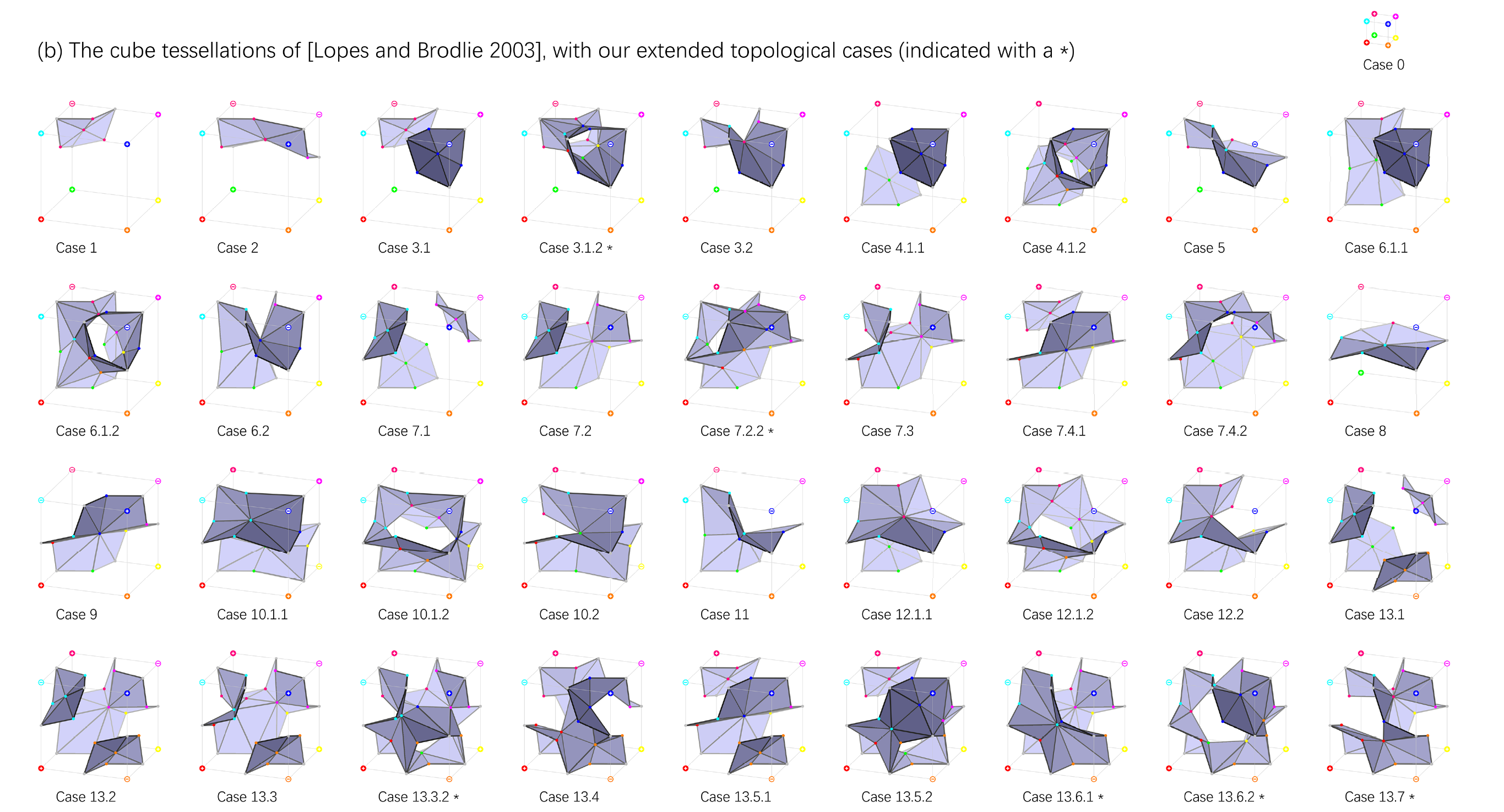
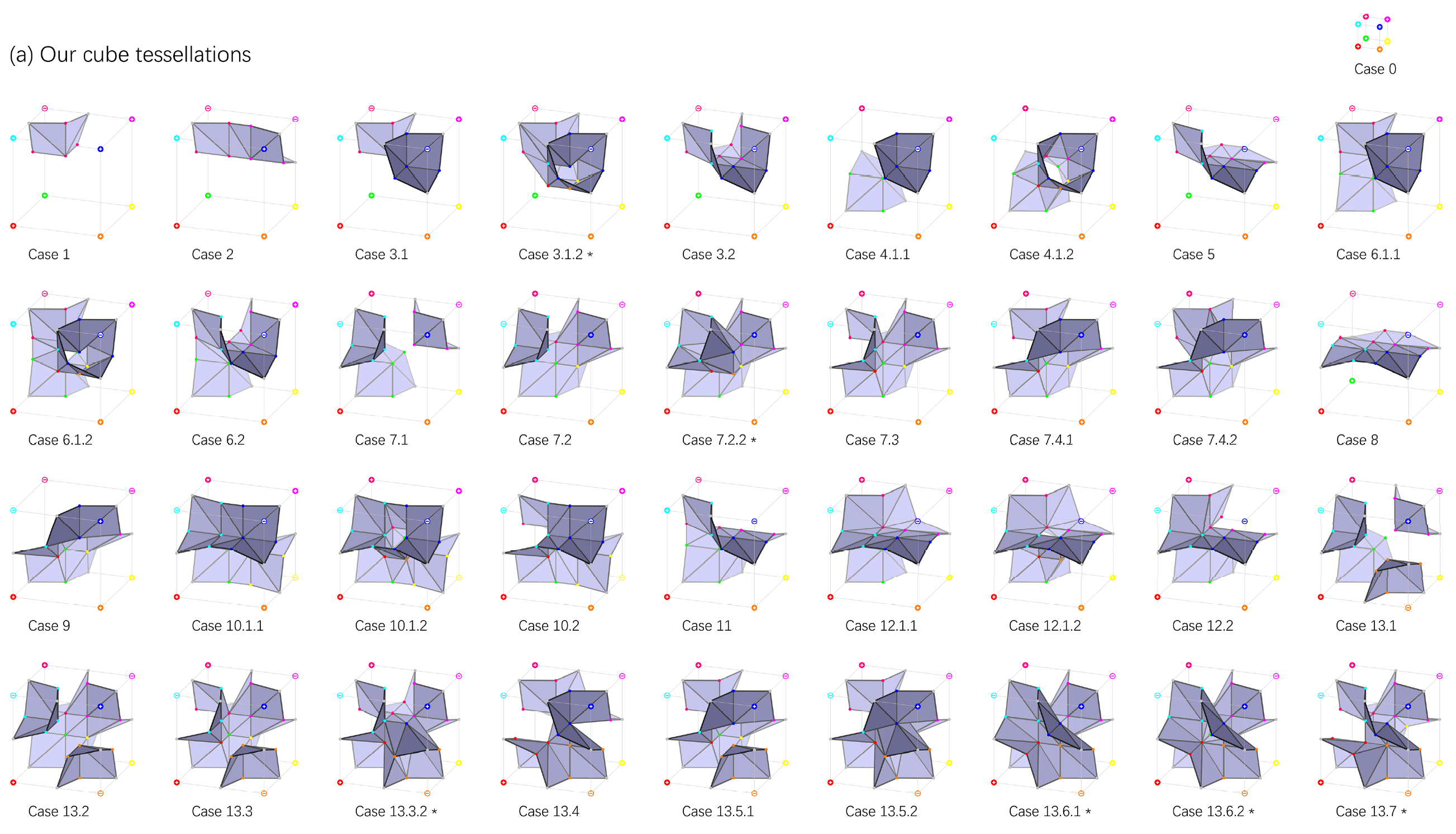
一个立方体八个顶点的数据已经编码成功,而论文对这样的数据与镶嵌模式进行对应时,也扩充了原有的情况数,在2003年的论文(对MC33进行了一定的修正)基础上,添加了6种管道类的镶嵌方案,被他们称作NMC-lite,而他们基于NMC-lite重新设计的结构叫做NMC。可能有人会好奇,$33+6=39\neq37$,那少的两种情况去哪了呢?这两种在论文中与其他的结构表达合并,故少了两种结构。
数据集的设计
由于网络需要输入距离场或体素,输出布尔值和浮点数向量,他们将物体按分辨率切分,对于每一个小立方体,按照以下次序去得到布尔值和浮点数的真实值(Ground Truth):
- 确定拓扑类型(布尔比特)
- 使用$9\times9\times9$的采样,判断各点正负,得到隐式距离场
- 通过采样的隐式距离场,判断每个面的顶点的连通性(相邻的采样点符号相同为相连)
- 通过检测立方体内部的连通块数量,判断是否有隧道,以及判断是否能表示
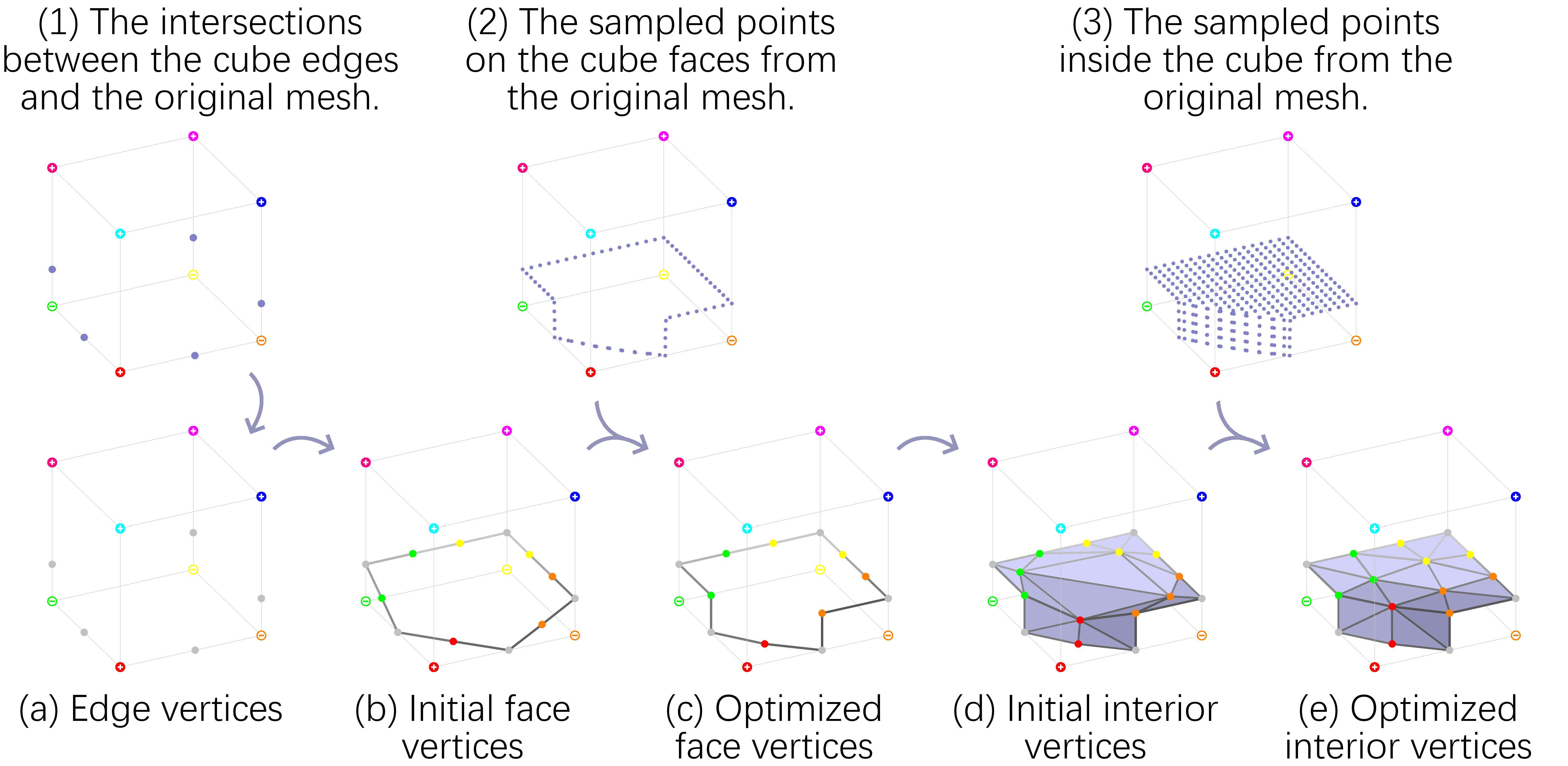
- 立方体与物体求交,获得所有立方体每条边与物体的交点(如果有)
- 对物体与立方体表面的交采样,确定所有立方体面片内点的位置
- 对物体与立方体的交进行采样,确定所有立方体内8个点(如果需要)的位置
深度学习网络相关
其实这篇论文并没有对深度学习网络进行优化,更多的贡献在于架构了几何表达到网络输入输出的结构关系。
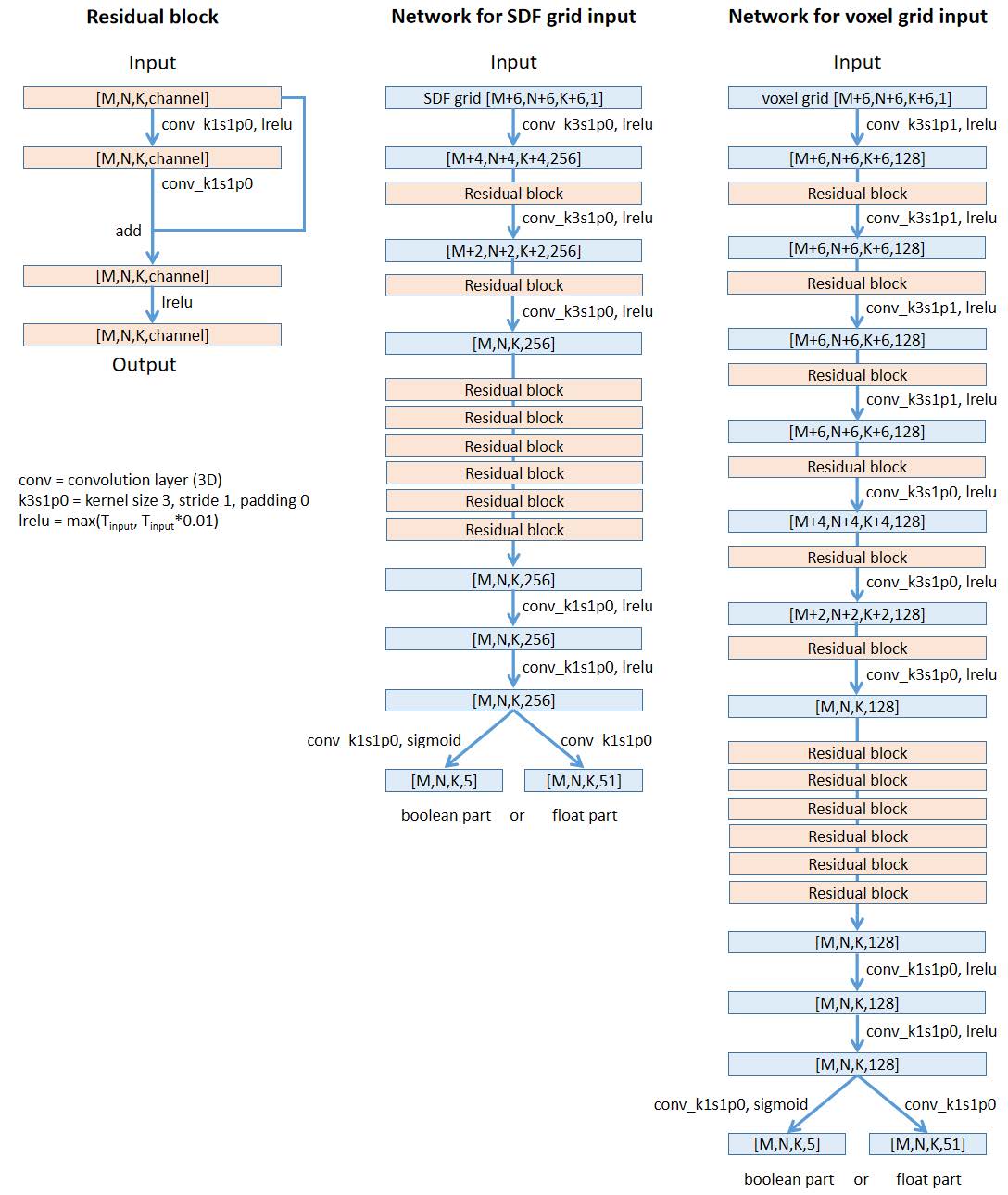
- 网络:3D ResNet
- Loss函数
- 对于布尔值结果使用BCE(Binary Cross Entropy)
- 对于浮点数部分使用MSE(Mean Square Loss)
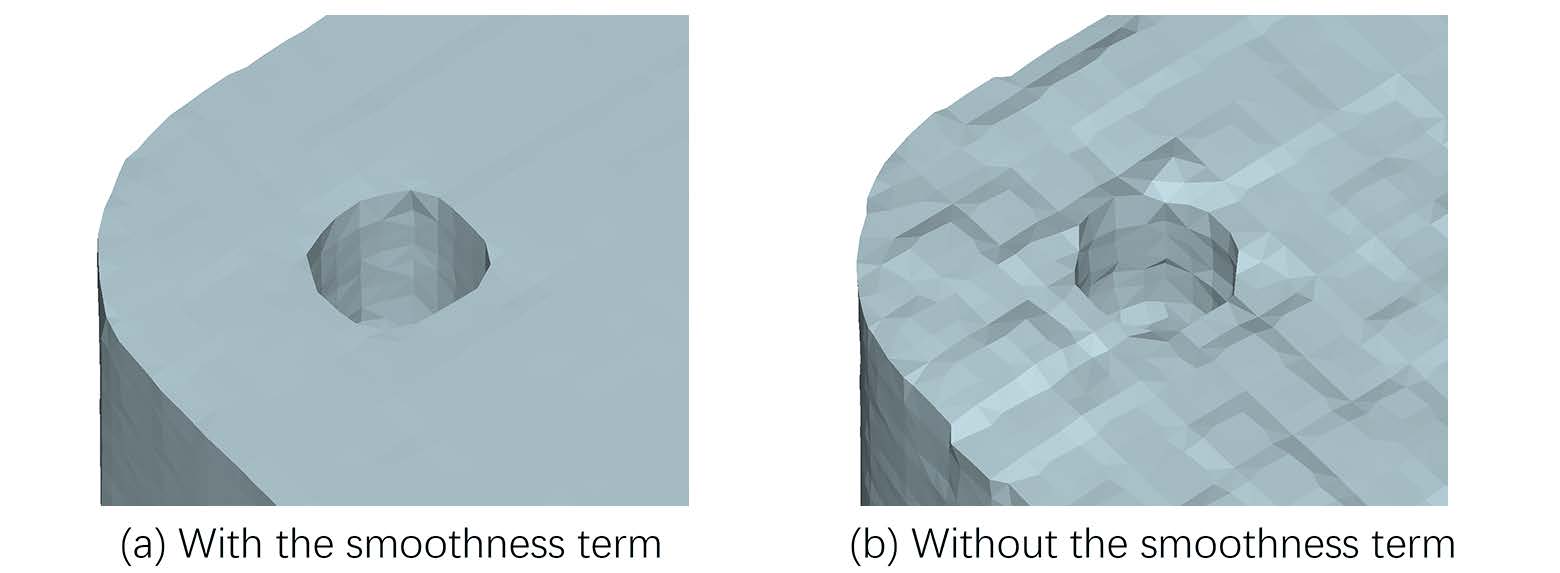
- 如果输入是voxel,为了让结果光滑,在浮点数部分Loss中额外加了光滑性loss(对于Ground Truth中的长度较短的Mesh中的边,计算其在预测模型中的长度。由于镶嵌模式是另一个网络计算,可以保证预测和真实模式相同,使得边是能对应的上的)
- 由于BCE和MSE的Loss权重不好设置,故用两个网络分别计算布尔值和浮点数
效果比对
- 论文其实给了许多的客观的评价指标,但是由于过于专业,本文仅从主观判断的角度展示结果。
- MNC的效果在所有分辨率的情况都优于MC33,但是随着分辨率的增长,NMC与MC33的差距会逐渐减小,因为每个立方体的拓扑情况会简化。从图片上来看,NMC的结果与MC33下一个精度的结果接近。
- NMC比MNC-lite效果好一些,但是三角形的数量要翻一番。
- 对于噪声的处理:如果把噪声的数据以正常数据的比例放入训练集和测试集,训练得到的模型效果会有明显的改善。


缺陷和未来工作
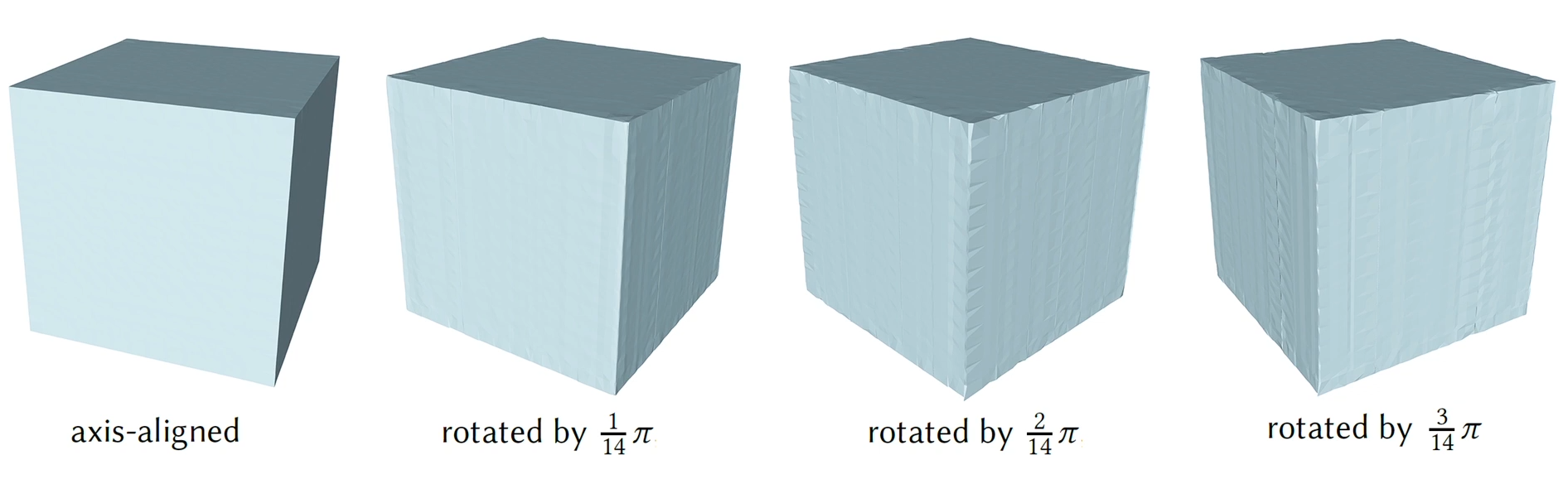
- 网络对于旋转是敏感的,因为他们训练的数据集的物体大多与坐标轴对齐,于是他们写的平滑项loss会驱使着向坐标轴对齐。
- 对于某些拓扑结构,匹配不到对应的镶嵌模板(主要是分辨率不够,使得拓扑结构复杂或极端)
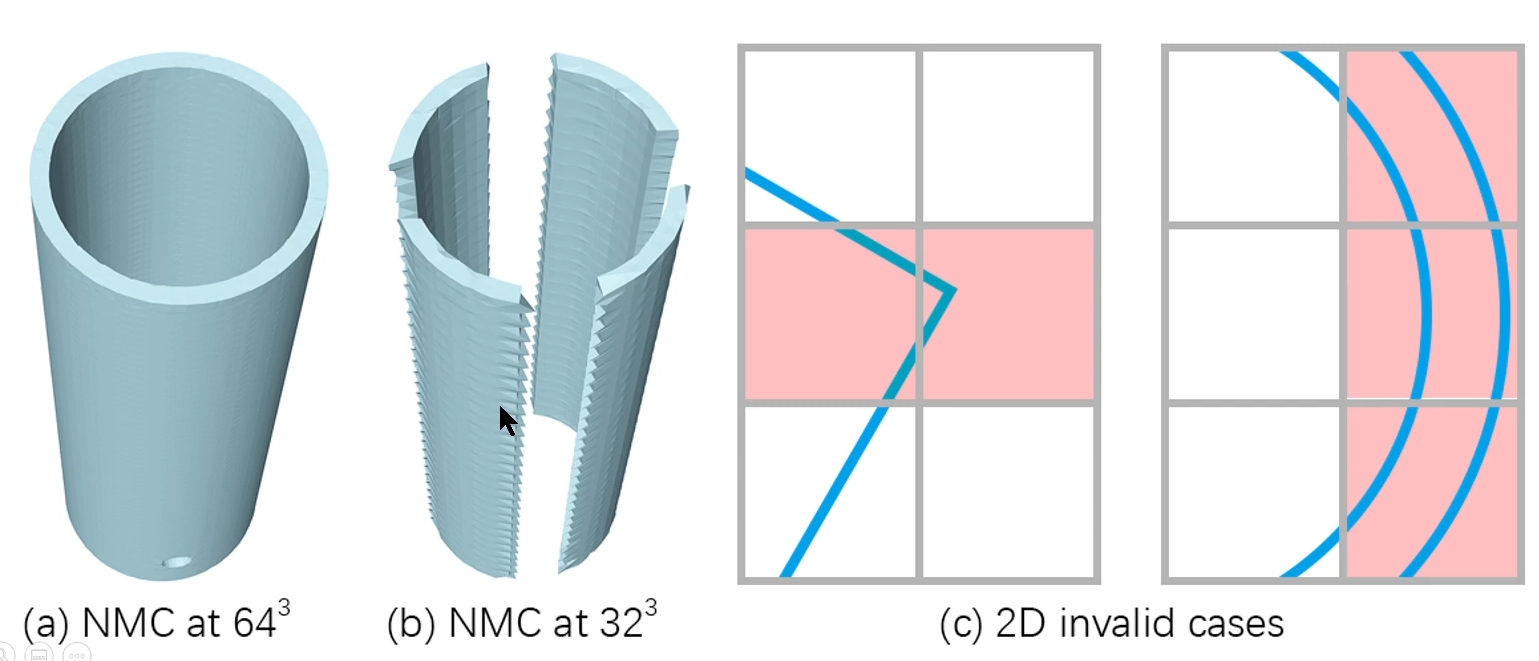
- 某些匹配不成功的立方体,所计算的结果可能有自交叉。